Medidas de posición

1- Introducción

La estadística descriptiva es una rama de las matemáticas muy utilizables al momento de realizar investigaciones cuantitativas, sobre una muestra representativa de un universo determinado.

La estadística descriptiva se sub divide en 3 medidas muy importantes, las cuales son:

– Medidas de tendencia central.

– Medidas de posición.

– Medidas de dispersión.

 

En este documento trabajaremos las medidas de posición.

 

2- Medidas de posición

Definición:
Las medidas de posición sirven para dividir una muestra determinada en una cierta cantidad de grupos con la misma cantidad de individuos.

– Cuartiles.

– Quintiles.

– Deciles.

– Percentiles.

Las más utilizadas son los cuartiles y percentiles, por lo tanto, trabajaremos con estas medidas en particular.

 

2.1- Cuartiles
Los cuartiles, como su nombre lo dice, divide la muestra en 4 grupos de igual magnitud (cantidad de individuos).

Si dividimos la muestra en cuartiles podemos tener solo 3 cuartiles (ya que el cuarto cuartil corresponde a la muestra completa)

a- Cuartil 1: $\left(Q_1\right)$: El primer cuartil abarca al 25% de la muestra o sea la primera cuarta parte de la muestra total.

 

 

b- Cuartil 2: $\left(Q_2\right)$: El segundo cuartil abarca el 50% de la muestra o sea la mitad de la muestra. Este cuartil corresponde a la mitad de la muestra o sea la mediana de la muestra.

 

 

Los cuartiles se pueden aplicar tanto para datos dispersos como los datos tabulados (agrupados).

Si queremos determinar algún determinado cuartil debemos aplicar la siguiente fórmula:

$Q_k=\frac{n·k}{4}$

Donde:

k = cuartil que se quiere determinar.
n = número total de datos de la muestra.

 

Primero trabajaremos con los cuartiles para datos dispersos:

 

Ejemplo 1:
Dado la siguiente secuencia estadística:

2 – 3 – 4 – 5 – 5 – 7 – 8 – 10 – 12 – 12 – 14 – 15 – 16 – 16 – 16 – 20 – 22 – 22

Determine los cuartiles.

 

Solución:
Primer paso para poder determinar cualquier medida de posición, debemos primero ordenar los datos de menor a mayor (sólo se ordenan para datos dispersos).

En este caso ya están ordenados, así que nos ahorramos ese paso.

Segundo paso es aplicar la fórmula de cuartil para poder determinar la posición de cada uno de los datos.

Para el primer cuartil nos queda:

 

$Q_1=\frac{18·1}{4}$

Recordemos que el 18 representa la cantidad total de datos de la muestra.

 

$Q_1=\frac{18}{4}\to 4,5$

Ese valor corresponde a la posición que utiliza el primer cuartil, es decir, el primer cuartil se sitúa en la posición 4,5 como sabemos la posición 4,5 está entre la posición 4 y la 5, por lo tanto, debemos sacar un promedio entre los datos que están en la posición 4 y 5 respectivamente, para poder determinar la posición aproximada del primer cuartil.

 

2 – 3 – 4 – 5 – 5 -7 – 8 – 10 – 12 – 12 – 14 – 15 – 16 – 16 – 16 – 20 – 22 – 22

 

Como vemos los datos que están en la posición 4 y 5 es el número 5 y, al determinar el promedio entre esos números, nos da el mismo 5.

Por lo tanto $Q_1=5$

 

Para el segundo cuartil nos queda:

 

$Q_2=\frac{18·2}{ 4}\to 9$

 

Entonces, el cuartil número dos está situado en la posición número 9 de la muestra. Este segundo cuartil lo vamos a determinar con otro color para poder diferenciarlos.

 

2 – 3 – 4 – 5 – 5 -7 – 8 – 10 – 12 – 12 – 14 – 15 – 16 – 16 – 16 – 20 – 22 – 22

 

Como vemos en la posición 9 está ubicado el primer número 12. Por lo tanto $Q_2=12$

 

Para el tercer cuartil nos queda:

 

$Q_3=\frac{18·3}{4}\to 13,5$

 

Entonces el cuartil número tres está situado en la posición número 13,5. Al igual que el primer cuartil esta posición se encuentra ubicada entre la posición 13 y la 14. Por lo tanto, debemos calcular un promedio con los valores que se encuentran en esa posición.

 

2 – 3 – 4 – 5 – 5 -7 – 8 – 10 – 12 – 12 – 14 – 15 – 16 – 16 – 16 – 20 – 22 – 22

 

Como nos damos cuenta en la posición 13 y 14 está ubicado el número 16. Por lo tanto, el promedio sigue siendo 16. Por lo tanto $Q_3=16$

En conclusión, los cuartiles nos quedan:

 

 

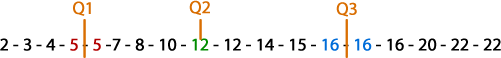
Como podemos ver la muestra está dividida en 4 grupos donde entran 4 datos y medio.

 

Segundo, determinaremos cuartiles para datos agrupados:

Cuando tenemos datos agrupados tenemos un inconveniente, ya que no podemos ordenar los datos de menor a mayor por el hecho de que ya están agrupados en una tabla. Por lo tanto, debemos aplicar una fórmula para poder estimar aproximadamente donde está el cuartil a determinar.

Si queremos determinar un cuartil determinado, debemos aplicar la siguiente fórmula:

 

$Q_k=L_i+\frac{ {\displaystyle \frac{n·k}{4}}–F_{i–1}}{f_i}·a_i$

 

Donde:

$L_i$= límite inferior del intervalo.
$n$= número total de la muestra.
$F_{i–1}$ = Frecuencia acumulada anterior.
$f_i$ = frecuencia absoluta del intervalo.
$a_i$= amplitud del intervalo.
$k$ = número de cuartil a calcular.

 

Ejemplo 2:

Calcule el primer cuartil de la siguiente distribución de frecuencias:

 

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

 

 

Solución:

Como en este caso tenemos los datos agrupados, entonces no podemos ordenarlos de menor a mayor, por lo tanto, debemos encontrar en que intervalo se encuentra el cuartil número 1.

 

Primer paso, determinar la posición del cuartil número 1. Para eso debemos aplicar.

 

$Q_1=\frac{65·1}{4}\to 16,25$

Por lo tanto, debemos encontrar el intervalo donde se encuentre la posición 16, entonces debemos ver en las frecuencias acumuladas en cuál de estas está incluida la posición 16.

Como se visualiza la tabla la frecuencia acumulada del segundo intervalo es 18. Por lo tanto, ya está incluido la posición 16. Entonces en ese intervalo está el cuartil número 1.

 

	fi	Fi
[50, 60)	8	8
[60, 70)	10	18
[70, 80)	16	34
[80, 90)	14	48
[90, 100)	10	58
[100, 110)	5	63
[110, 120)	2	65
	65

 

 

 

Ahora podemos determinar los datos que nos pide la fórmula, tomando en cuenta el intervalo donde se encuentra el cuartil número 1.

Límite inferior: el límite inferior es el extremo donde parte el intervalo donde se encuentra el cuartil. En este caso el extremo inferior es de 60.

$L_I=60$

La frecuencia acumulada anterior, como su nombre lo dice, es la que se encuentra sobre la frecuencia acumulada del intervalo donde está el cuartil número 1.

$F_{i–1}=8$

La frecuencia del intervalo, como se dice, es la frecuencia que se encuentra en el intervalo. 

$f_i=10$

 
La amplitud es la diferencia de los extremos del intervalo.

$a=10$

 

Ahora vamos a reemplazar en la fórmula quedando:

 

$$\begin{gathered} Q_1=60+\frac{16,25–8}{10}·10 \\ {Q}_1=60+8,25 \\ {\mathit{Q}}_{\mathbf{1}}\mathbf{=}\mathbf{68}\mathbf{,}\mathbf{25} \end{gathered}$$

 

Eso quiere decir que el primer 25% de la muestra está bajo el intervalo 70.

 

 

2.2- Percentiles
Los percentiles dividen la muestra en 100 partes iguales la magnitud de la muestra.

Si dividimos en percentiles podemos dividir la muestra en 99 veces, ya que el percentil 100 corresponde a la totalidad de la muestra.

Cada uno de estos percentiles corresponde a un 1% de la muestra total.

P₁= corresponde al primer 1% de la muestra.

P₂= corresponde al 2% de la muestra.

P₃= corresponde al  3% de la muestra.

P₉₉= corresponde al 99% de la muestra.

 

Si queremos determinar algún percentil, debemos aplicar la siguiente formula:

 

$P_k=\frac{N·k}{100}$

Ejemplo 1: 
A continuación, se muestran las notas obtenidas de un alumno en una asignatura. Determine el percentil 80. Interprete resultado.

2    2    6    6    5    6    7    6    2    4
3    7    6    3    7    6    5    5    7    2
7    3    6    6    4    4    6    6    6    3
2    4    6    4    4    7    6    3    2    7
4    7    2    3    3    3    6    6    2    4
6    4    6    2    2    3    3    5    3    6
6    3    3    3    6    6    5    7    4    2
7    6    4    5    2    6    7    3    5    3
4    3    2    2    7    2    7    2    6    5
4    6    5    7    3    3    6    3    3    6

 

 

Solución:
En este caso, para poder determinar el percentil pedido debemos ordenar los datos de menor a mayor, “recordar que sólo se ordenan cuando los datos están dispersos y no cuando están tabulados”.

Ordenando los datos nos queda:

 

$$\begin{gathered} 2–2–2–2–2–2–2–2–2–2–2–2–2–2–2–2– \\ 3–3–3–3–3–3–3–3–3–3–3–3–3–3–3–3– \\ 3–3–3–3–3–4–4–4–4–4–4–4–4–4–4–4– \\ 4–4–5–5–5–5–5–5–5–5–5–6–6–6–6–6– \\ 4–4–5–5–5–5–5–5–5–5–5–6–6–6–6–6– \\ 6–6–6–6–6–6–7–7–7–7–7–7–7–7–7–7– \\ 7–7–7–7 \end{gathered}$$

Ahora debemos determinar la posición donde se encuentra el percentil 80.

$$\begin{gathered} P_k=\frac{N·k}{100} \\ {P}_{80}=\frac{80·100}{100} \\ {P}_{80}=80 \end{gathered}$$

Es decir, el percentil 80 está en la posición 80. Si nos fijamos en la posición 80 está la nota número 6.0.

 

Con respecto a la conclusión podemos decir:

– El 80% de las notas de los alumnos son menores o iguales a la nota 6.0., ya que hasta la nota 60 tenemos el 80% de las notas.

 

Pero también podemos realizar el análisis tomando en cuenta el 20% restante:

– Sólo el 20% de las notas son desde un 6.0 hasta un 7.0 Inclusive.

 

Si queremos determinar un percentil para datos agrupados, debemos aplicar la siguiente fórmula:

$P_k=L_i+\frac{{\displaystyle \frac{n·k}{100}}–F_{i–1}}{f_i}·a_i$

Como se puede visualizar es la misma fórmula que la de cuartil, la única diferencia es que se divide en 100 (por que dividiremos la muestra en 100).

Ahora determinaremos percentiles para datos agrupados.

Ejemplo 4:
Se ha pasado un test de 80 preguntas a 600 personas. El número de respuestas correctas se refleja en la siguiente tabla:

 

Respuestas correctas	Número de personas
[0,10)	40
[10, 20)	60
[20, 30)	75
[30, 40)	90
[40, 50)	105
[50, 60)	85
[60, 70)	80
[70, 80)	65

Determine el percentil 85.

Solución:
Como queremos determinar el percentil, lo primero que debemos determinar es la frecuencia acumulada, quedando:

 

Respuestas correctas	ni	Ni
[0,10)	40	Comparte este contenido: Todo el contenido y material en este sitio es propiedad de Wited y está protegido por derechos de autor. La reproducción, distribución o uso sin permiso está prohibida y es ilegal. Se permite la referencia sin uso comercial solo con atribución adecuada y enlace a la fuente original. Fecha de publicación: 06/03/2024 Última edición: 06/04/2024 Te recomendamos seguir estudiando estos temas Círculo y circunferencia: área, perímetro y longitud Ver contenido Dramatizar Ver contenido Elementos secundarios del triángulo: simetrales y transversales de gravedad Ver contenido Comienza hoy Iniciar sesión Contáctate con nuestro equipo comercial Completa tus datos y cuéntanos para qué te gustaría cotizar Wited Nombre Tipo Para mi empresa Para mis hijos Para mi colegio Para homeschool Correo Mensaje Enviar No tienes acceso a este recurso Para usar este recurso necesitas iniciar sesión o crear una cuenta. Ver planes Iniciar sesión Resuelve tus dudas con los profesores de Wited Crea tu cuenta o inicia sesión para que nuestros profesores te ayuden Ver planes Iniciar sesión Escribe tu pregunta *Necesitas una cuenta para hacer preguntas Ayuda con tareas y estudios Chat y videollamadas con profesores Max AI para resolver dudas Contenidos curriculares por nivel Ejercicios para practicar lo aprendido Cursos de reforzamiento Cursos extraprogramáticos Recursos digitales Cuenta para padres/supervisor Informes de rendimiento MaxPoints 3000 Trimestral USD $46 /3 meses Inscripción