1- Definición
Un diagrama de dispersión o nube de puntos es un gráfico que utiliza el plano cartesiano para poder representar los valores de dos variables para un mismo conjunto de datos.
Generalmente estos diagramas sirven para representar una población o muestra en función de dos variables distintas.
Por ejemplo, podemos tomar una muestra de alumnos de un curso y comparar los promedios de dos asignaturas, al ser dos asignaturas ya estamos en frente de una distribución bidimensional (dos dimensiones o variables).
2- Como realizar un diagrama de dispersión
Primer paso: Determinar cuál es la situación que vamos a estudiar. Ya que, si no logramos comprender la situación, no podremos ser capaz de determinar las variables a estudiar.
Segundo paso: Determinar las variables a utilizar. Para esto es necesario que logremos comprender si existe alguna relación entre estas variables.
Tercer paso: Recolectar los datos relacionados a las variables que vamos a estudiar. Es de suma importancia estos datos ya que en base a estos podremos graficar el diagrama de dispersión.
Cuarto paso: Ubicar los pares ordenados (x,y) en el plano cartesiano, recuerda que una variable debe estar representado en el eje de las abscisas y el otro en el de las ordenadas.
Ejemplo 1:
Una empresa quiere abrir una nueva área de producción para la impresión de posters, y en este momento están realizando todos los ensayos y pruebas para así poder determinar la cantidad de tinta de cada color que deberían tener las maquinas.
Para la prueba inicial han decidido establecer la relación de errores de impresión según el grado de llenado de los recipientes de tinta de la máquina.
El departamento de control de calidad durante 40 días ha hecho pruebas arrojando los siguientes resultados:
|
Cantidad de tinta (Litros) |
Número de errores |
|
0,47 |
16 |
|
0,48 |
14 |
|
0,69 |
30 |
|
0,7 |
31 |
|
0,59 |
15 |
|
0,59 |
17 |
|
0,37 |
10 |
|
0,62 |
21 |
|
0,39 |
11 |
|
0,35 |
13 |
|
0,68 |
28 |
|
0,52 |
17 |
|
0,42 |
11 |
|
0,51 |
18 |
|
0,5 |
19 |
|
0,34 |
10 |
|
0,41 |
14 |
|
0,3 |
7 |
|
0,53 |
20 |
|
0,33 |
7 |
|
0,36 |
11 |
|
0,4 |
16 |
|
0,4 |
13 |
|
0,69 |
24 |
|
0,61 |
24 |
|
0,32 |
9 |
|
0,66 |
28 |
|
0,64 |
23 |
|
0,45 |
17 |
|
0,59 |
20 |
|
0,6 |
21 |
|
0,56 |
19 |
|
0,6 |
20 |
|
0,55 |
18 |
|
0,44 |
15 |
|
0,49 |
16 |
|
0,63 |
25 |
|
0,65 |
26 |
|
0,38 |
10 |
|
0,67 |
24 |
Realice el diagrama de dispersión.
Solución:
Seguiremos los pasos descritos anteriormente para poder graficar la nube de puntos. Nos saltaremos el primer paso ya que la situación ya está descrita.
Segundo paso: Las variables a utilizar serán: cantidad de tinta y números de errores.
Tercer paso: En la recolección de datos, este paso ya está realizado debido a que el enunciado entrega los datos de las variables. Así que utilizaremos la tabla entregada por el departamento de control de calidad.
Cuarto paso: Al representar los puntos en el plano cartesiano, debemos recordar que los pares ordenados son: (x,y) . En el eje de las abscisas estará la variable litros de tinta y en el eje de las ordenadas estará la variable número de errores.
Quinto paso: Solo debemos graficar cada uno de los puntos que se generan al cruzar los pares ordenados. Quedando una gráfica como la siguiente:
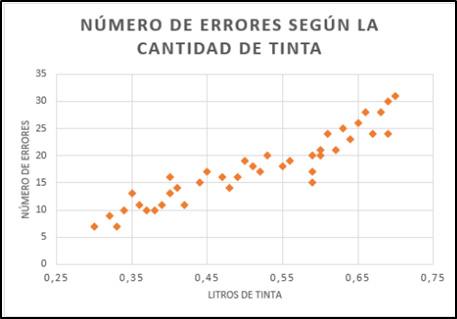
Una vez hecho el grafico de dispersión podemos visualizar una nube de puntos, de aquí viene el nombre del gráfico. Ya que su representación son diversos puntos en el plano cartesiano.
3- Correlación
Una vez hecha la gráfica podemos determinar qué tipo de relación tienen las variables que se quieren estudiar para un mismo grupo de estudio. Esta correlación se puede clasificar en:
3.1- Positiva:
Un diagrama de dispersión tiene una correlación positiva cuando las variables están en proporcionalidad directa. Es decir, ambas aumentan o disminuyen a la vez.
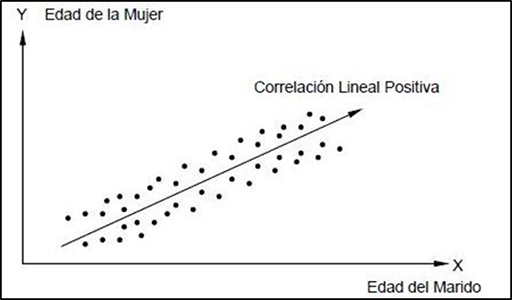
Para poder darnos cuenta si la dispersión tiene una relación positiva podemos trazar una recta imaginaria desde el origen.
Nos daremos cuenta que la línea tiene un sentido positivo como se visualiza en la imagen anterior.
Ejemplos:
Existe una correlación positiva entre las variables: altura de una persona y tamaño del pie, ya que si la altura aumenta el tamaño del pie igual.
Así mismo si queremos representar las variables kilómetros recorrido y combustible utilizado. También tienen una correlación positiva, ya que si aumenta los kilómetros recorridos también aumentan el combustible utilizado.
3.2- Negativa:
Un diagrama de dispersión tiene una relación negativa cuando las variables están con proporcionalidad inversa. Es decir, si una variable aumenta la otra disminuye y viceversa.
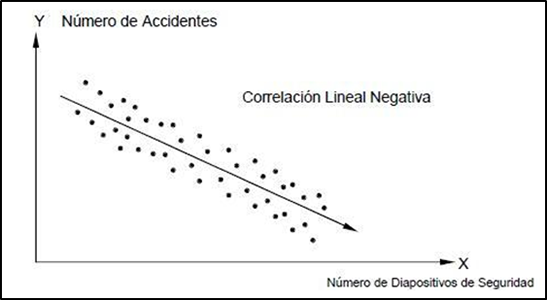
Para poder darnos cuenta si la dispersión tiene una relación negativa basta con observar la recta trazada, si ésta tiene pendiente negativa, es decir desciende, entonces la correlación es negativa.
Ejemplos:
Si queremos representar las variables horas de estudio y horas de juego. Estamos al frente de una correlación negativa, ya que al aumentar las horas de estudio disminuyen las horas de juego y lo mismo ocurre al revés.
También ocurre esto si queremos representar las variables número de accidentes en un trabajo y número de dispositivos de seguridad, si los dispositivos aumentan disminuye el número de accidentes en un trabajo.
3.3 – Sin correlación:
Un diagrama de dispersión se denomina sin correlación, cuando las variables no tienen relación alguna ya que en el grafico no se puede visualizar ningún patrón en común. Y esto ocurre por la nula relación que tienen las variables.
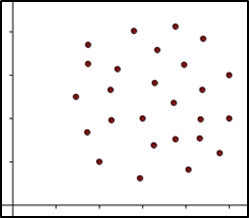
Ejemplos:
Si queremos representar las variables puntos en un video juego y el número de calzado de pies. Estas variables no tienen ninguna relación entre si ya que si aumentan los puntos en un video juego no influye en nada al número de calzado de pies. Por lo tanto, se dice que estas variables no tienen correlación.
4- Grado de correlación
El grado de correlación, indica cual es la proximidad que tienen los puntos unos con otros en la nube de puntos.
Podemos tener 2 tipos:
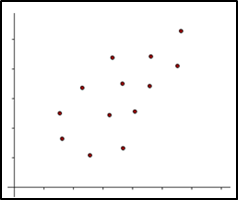
4.1- Fuerte:
La correlación tiene un grado fuerte cuando los puntos están más cercas unos a otros y a la recta que se traza para visualizar el tipo de correlación que tienen las variables.

4.2- Débil:
La correlación tiene un grado débil cuando los puntos están más alejados unos de otros y a la recta que se traza para visualizar el tipo de correlación que tienen las variables.
5- Datos atípicos
Cuando uno quiere determinar si la correlación entre las variables es positiva o negativa, como se mencionó debemos dibujar una recta y ver el sentido de esta para poder determinar si las variables tienen una correlación positiva o negativa.
Pero siempre van a existir datos que se alejan mucho de las rectas, aunque la mayoría este cerca de esta recta. Estos puntos son conocidos como datos atípicos.
En palabras simples los datos atípicos son aquellos que no siguen el patrón de los demás datos.
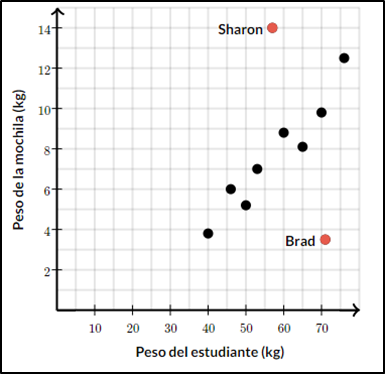
Como se ve en el diagrama los puntos que están de color rojo están alejados a los demás datos, estos puntos rojos son los conocidos datos atípicos ya que no siguen el mismo patrón que los demás puntos.
Ejemplo 2:
Los siguientes datos representan los años de práctica profesional y el ingreso anual. En millones de pesos.
|
Años de práctica |
Ingresos |
|
5 |
4 |
|
15 |
4 |
|
24 |
9 |
|
16 |
7 |
|
19 |
6 |
A) Realice el diagrama de dispersión.
B) Determine el tipo de correlación entre las variables.
C) Determine el grado de correlación entre estas variables.
D) Determine si existen o no datos atípicos.
Solución:
A)
Primero vamos a determinar las variables a estudiar las cuales son:
– Años de práctica
– Ingresos
Como sabemos dependiendo de la cantidad de años de práctica es el ingreso, por lo tanto, en el eje de las abscisas estará la variable años de práctica y en el eje de las ordenadas estará la variable ingresos.
Ahora determinaremos los pares ordenados a graficar los cuales son:
(5,4); (15,4); (24,9); (16,7); (19,6)
Realizando la gráfica en el plano cartesiano nos queda:
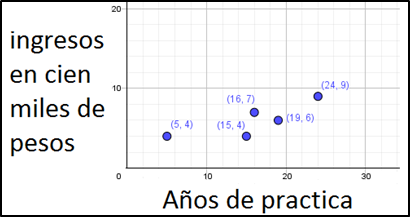
B)
Para poder determinar el tipo de correlación debemos ver si ambas variables aumentan o ambas disminuyen (positiva), si solo aumenta una y la otra disminuye (negativa) o si no existe ninguna correlación.
Para eso podemos trazar una recta desde el origen y poder ver el sentido de la recta.
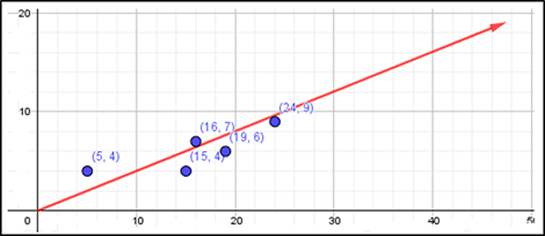
Como se visualiza estas variables tienen una correlación positiva.
C)
El grado de la correlación es fuerte ya que como se visualiza los datos están muy cercanos unos a otros.
D)
El único dato atípico que se puede visualizar es el punto (5,4). Ya que está alejado al resto de los puntos.
Ejemplo 3:
Un estadístico de una determinada línea aérea desea determinar la ecuación que relaciona la distancia de destino con la carga de mercancía para un tamaño estándar de embalaje. Para una muestra aleatoria de 10 facturaciones de carga, se obtuvieron los siguientes datos:
|
Distancia |
Carga |
|
22.4 |
6.8 |
|
36.8 |
10.5 |
|
14.4 |
4.0 |
|
27.2 |
7.9 |
|
16.0 |
8.1 |
|
35.2 |
9.5 |
|
8.0 |
3.1 |
|
19.2 |
7.2 |
|
9.6 |
4.5 |
|
25.6 |
9.3 |
Determine:
A) Diagrama de dispersión (nube de puntos)
B) Tipo de correlación entre las variables.
C) Grado de correlación.
D) Determine si existen datos atípicos.
Solución:
A)
Primero determinaremos las variables a estudiar en este caso son:
– Distancia
– Carga
Como sabemos dependiendo de la distancia es la carga que debe tener la línea aérea. Entonces en el eje de las abscisas estará la variable distancia y en el eje de las ordenadas estará la variable de carga.
Ahora determinaremos los pares ordenados a graficar los cuales son:
(22,4 ; 6,8); (36,8 ; 10,5); (14,4 ; 4); (27,2 ; 7,9); (16 ; 8,1); (35,2 ; 9,5)
(8 ; 3,1); (19,2 ; 7,2); (9,6 ; 4,5); (25,6 ; 9,3)
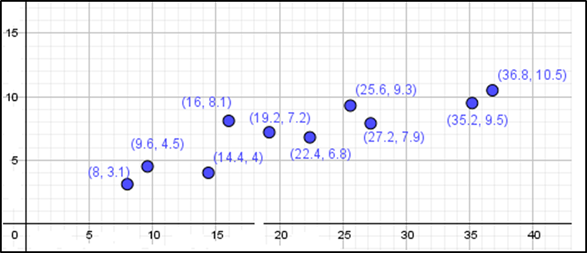
B)
Para poder determinar el tipo de correlación debemos ver si ambas variables aumentan o ambas disminuyen (positiva), si solo aumenta una y la otra disminuye (negativa) o si no existe ninguna correlación.
Para eso podemos trazar una recta desde el origen y poder ver el sentido de la recta.
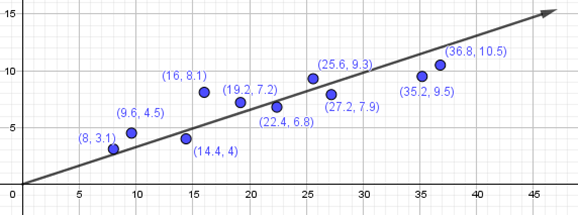
Como se visualiza tienen una correlación positiva estas variables.
C)
Para determinar el grado de correlación, nos damos cuenta de que tienen una fuerte correlación ya que están muy cerca unos de otros.
D)
En este caso el dato atípico es el punto (16; 8,1)

