Descomposición aditiva y multiplicativa de un número

1- Composición aditiva

A través de las sumas de 3 + 4, 5 + 2, 6 + 1 puede formarse el número 7. Así como las sumas de 12 + 3, 14 + 1 el número 15. Debes tener presente que para números de 2 cifras se estudia de preferencia la composición a partir de decenas. Por ejemplo:
 

.

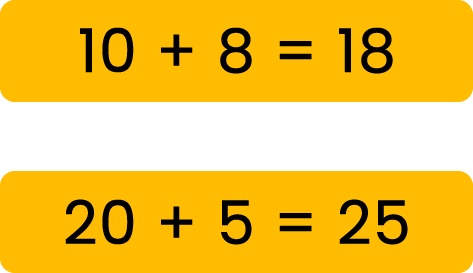
Veamos un ejemplo de composición aditiva en la vida cotidiana:

Marta está contando el dinero que tiene, para ello agrupó sus monedas y billetes:
 

 

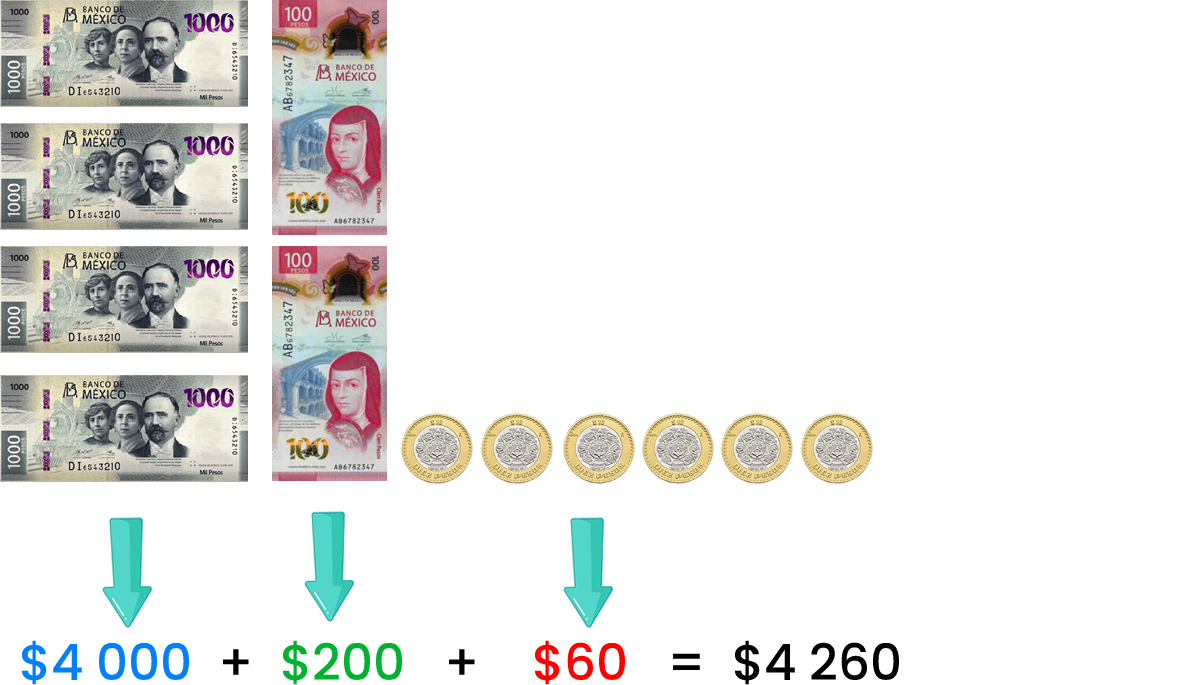
Ella tiene 4 billetes de $1 000, 2 de $100 y 6 monedas de $10.
Entonces, Marta tiene en total $4 260.

 

2- Descomposición aditiva

¿Sabías que un número cualquiera puede expresarse a través de una suma? Por ejemplo, el número 9 puede descomponerse en sumas tales como 4 + 5, 6 + 3, 8 + 1.

2.1- Descomposición aditiva canónica o estándar
Al igual que en la composición de números, se puede realizar una descomposición aditiva utilizando dinero.

Por ejemplo, para formar el número $4 650, utilizaremos billetes de $1 000 y $100 para representar las unidades de millar y las centenas respectivamente. Mientras que utilizaremos las monedas de $10 para representar decenas.

 

 

 

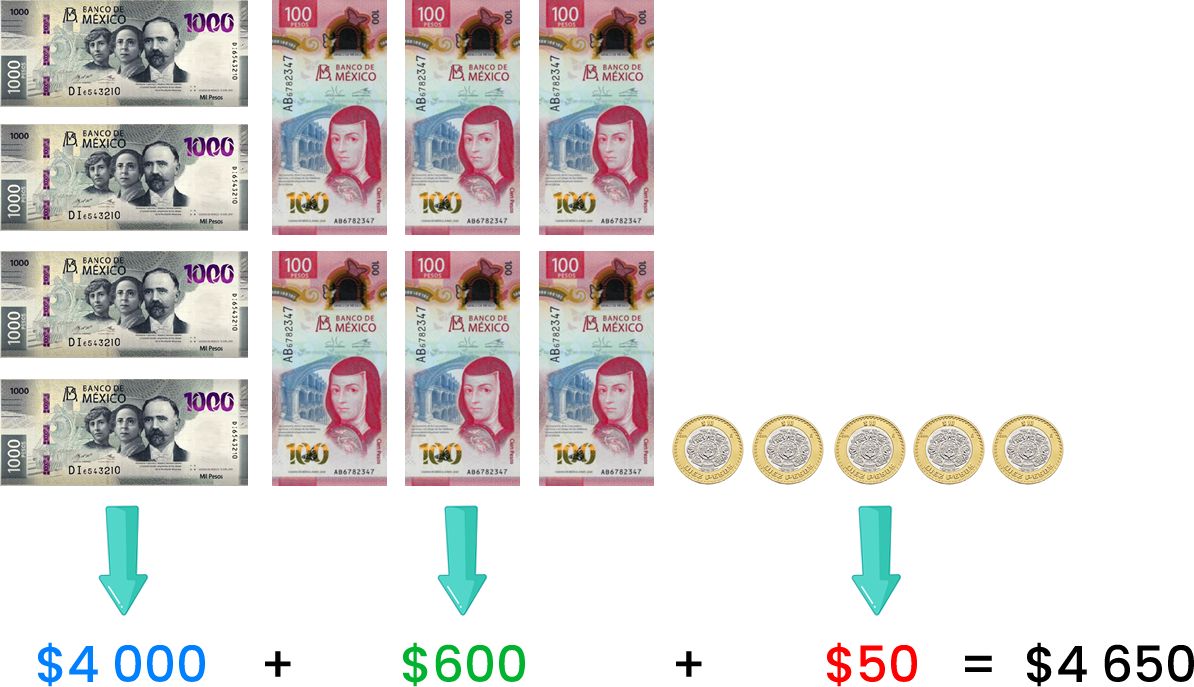
Entonces, 4 650 se puede descomponer aditivamente de la siguiente manera: 4 000 + 600 + 50.

Como puedes ver la descomposición aditiva canónica, que corresponde a descomponer los números como la suma de un múltiplo de 10 y el dígito correspondiente.

Ejemplo 1
Descompón el número 678 456 según su valor de posición.

Paso 1: Determina el valor posicional de cada dígito.

 

 

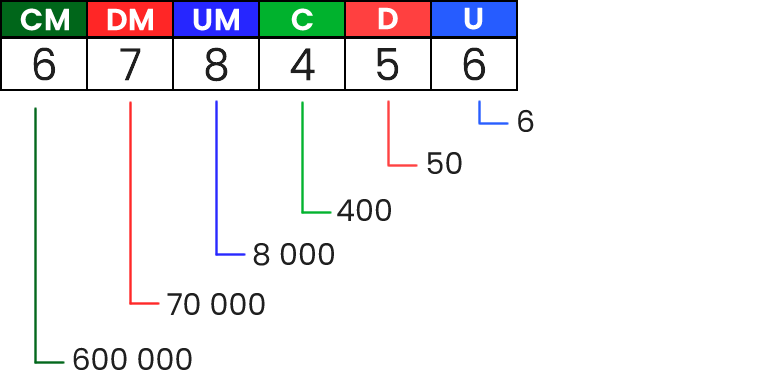
Paso 2: Expresa como sumandos los valores posicionales de cada dígito.
 

 

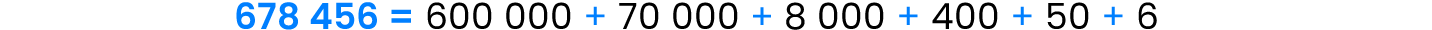
Ejemplo 2
Expresa de forma estándar el número 32 543 218.
En este caso, se debe realizar el mismo procedimiento anterior.
Se determina el valor de posición de cada dígito del número 32 543 218 y se expresan como sumandos.
 

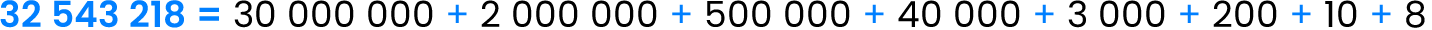
Ejemplo 3
Descompón el número 34 602 070 según su valor de posición.
En el caso que haya dígitos ceros en un número, no es necesario escribir el sumando asociado con esa posición.
 

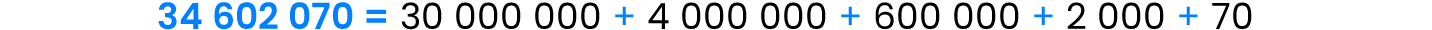
Estas formas de descomponer los números son especialmente recomendables para reforzar el conocimiento de la estructura del sistema de numeración decimal y para la comprensión de que el valor de un dígito depende de la posición que ocupe en el número. 

 

 

Por ejemplo, si descomponemos según el nombre de la posición de cada dígito los números:
 

 

2.2- Composición y descomposición aditiva de números con constructores numéricos
Los constructores numéricos constan de 9  tarjetas del 0 al 9 para las unidades, 9 tarjetas del 10 al 90 para las decenas, 9 tarjetas del 100 al 900 para las centenas y 9 tarjetas del 1000 al 9000  para las unidades de mil. En este caso, también incluiremos tarjetas para las posiciones más altas:

Al superponer las tarjetas se pueden componer números.

Ejemplo 1
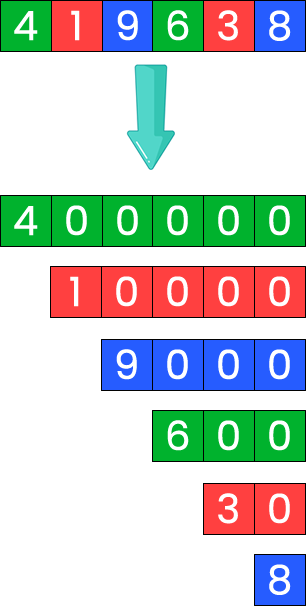
Para componer el número 419 638 se necesitan las tarjetas 400 000, 10 000, 9 000, 600, 30 y 8.
 

Para descomponer números aditivamente se quitan las tarjetas superpuestas:
 

 

 

Ejemplo 2
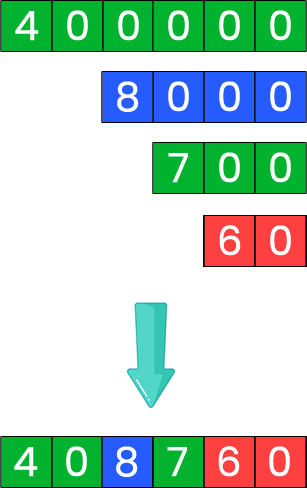
Para componer el número 408 760 se necesitan las tarjetas 400 000, 8 000, 700 y 60.
 

 

3- Descomposición expandida o multiplicativa

Otra forma de descomponer un número es expresarlo como una adición en que sus términos corresponden a la multiplicación de cada uno de sus dígitos por 1, 10, 100, 1 000, etc., según su valor posicional.

Recuerda que al multiplicar por números que son múltiplos de 10, puedes quitarle los ceros a uno de los factores, luego multiplicas las cifras. Finalmente, le añades los ceros al resultado.

Ejemplo: 6 $\times$100 000

Primero multiplicas 6$\times$1 = 6 y al resultado le añades los 5 ceros de 100 000.
Se forma el número 600 000.
 

 

 

Por ejemplo:

6 345 = 6 $\times$ 1 000 + 3 $\times$ 100 + 4 $\times$ 10 + 5 $\times$ 1

304 255 = 3 $\times$ 100 000 + 4 $\times$ 1 000 + 2 $\times$ 100 + 5 $\times$ 10 + 5 $\times$ 1

7 075 002 = 7 $\times$ 1 000 000 + 7 $\times$ 10 000 + 5 $\times$ 1 000 + 2 $\times$ 1

4 750 600 = 4 $\times$ 1 000 000 + 7 $\times$ 100 000 + 5 $\times$ 10 000 + 6 $\times$ 100

784 020 000 = 7 $\times$ 100 000 000 + 8 $\times$ 10 000 000 + 4 $\times$ 1 000 000 + 2 $\times$ 10 000

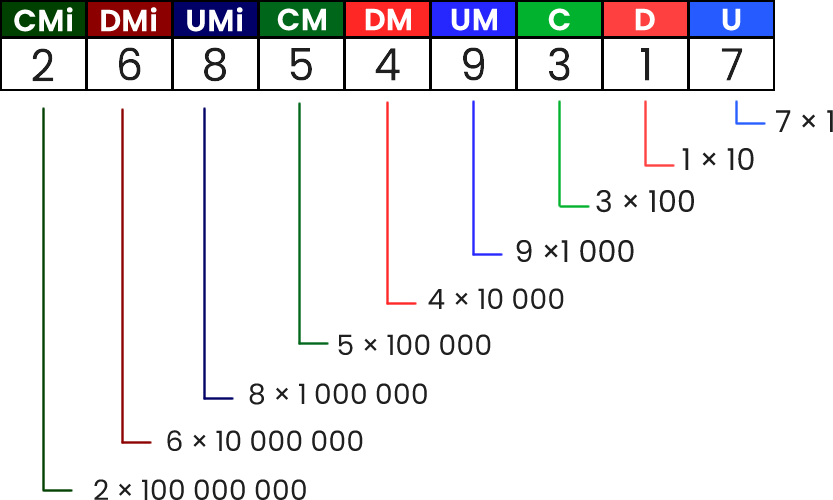
247 063 060 = 2 $\times$ 100 000 000 + 4 $\times$ 10 000 000 + 7 $\times$ 1 000 000 + 6 $\times$ 10 000 + 3 $\times$ 1 000 + 6 $\times$ 10 

 

3.1- Expresar la notación estándar de un número en notación expandida y viceversa
A partir de la notación estándar se puede expresar el número en su notación expandida, multiplicando los números.

Ejemplo:

342 056 090
 

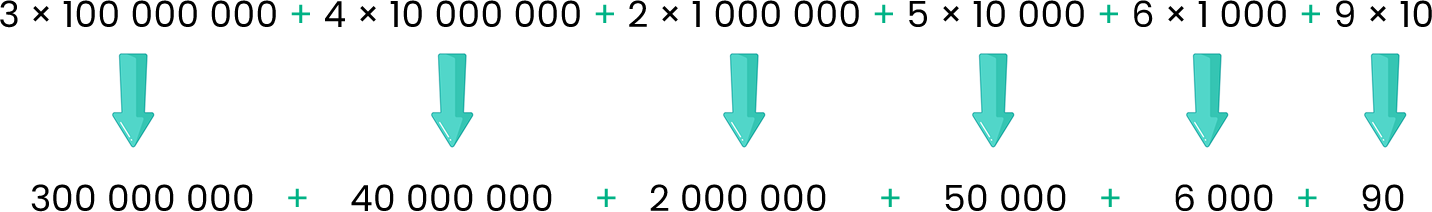
También ocurre el caso contrario, se puede expresar la notación estándar como notación expandida.

Ejemplo: 50 268 049
 

 

 

Entonces un número puede descomponerse:

Según el nombre de la posición de cada dígito. 

Ejemplo: 940 208 → 9CM + 4DM + 2C + 8U

En forma aditiva, según el valor posicional.

Ejemplo: 940 208 → 900 000 + 40 000 + 200 + 8

En forma multiplicativa.

Ejemplo: 940 208 → 9 $\times$ 100 000 + 4 $\times$ 10 000 + 2 $\times$ 100  + 8 $\times$ 1

 

 

4- Ejercicios

4.1- Descompone de manera estándar cada número, siguiendo los ejemplos anteriores:

a) 56 284 300 = 50 000 000 + 6 000 000 + 200 000 + 80 000 + 4 000 + 300
b) 7 903 605 = 7 000 000 + 900 000 + 3 000 + 600 + 5
c) 134 701 820 = 100 000 000 + 30 000 000 + 4 000 000 + 700 000 + 1 000 + 800 + 20

 

4.2- ¿Qué número representa cada una de estas expresiones?

a) 3 $\times$ 1 000 000 + 1 $\times$ 100 000 + 5 $\times$ 100 + 3 $\times$ 1 = 3 100 503
b) 4 $\times$ 10 000 000 + 7 $\times$ 10 000 + 2 $\times$ 1 000 + 9 $\times$ 10 = 40 072 090
c) 9 $\times$ 100 000 + 4 $\times$ 10 000 + 2 $\times$ 100 + 8 $\times$ 1 = 

Solucionario
 

4.1
a) 50 000 000 + 6 000 000 + 200 000 + 80 000 + 4 000 + 300
b) 7 000 000 + 900 000 + 3 000 + 600 + 5
c) 100 000 000 + 30 000 000 + 4 000 000 + 700 000 + 1 000 + 800 + 20

 

4.2
a) 3 100 503
b) 40 072 090
c) 940 208